Category: Numbers & Statistics

Sick Of The Exaggeration

Lies and Untruths, Numbers & Statistics

From Stephen Green (and a veritable host of others):

“The Democrats have a destructive addiction to the 20% side of a whole host of 80/20 issues.”

I can’t remember who first uttered the “80/20 issues” trope, but I’ll bet it was a Democrat like James Carville or Bill Maher.

With all things, scale matters.

Are you telling me that 20% of voters — that’s one in every five voters — supports:

  • men competing in women’s sports
  • gender-reversal surgery on minor children without parental notification (let alone consent)
  • not expelling criminal illegal aliens
  • not ending the flood of illegal immigrants who draw money from public health- and education services, at the expense of U.S. citizens
  • deficit spending and a ballooning national debt
  • a voting system that enables voter fraud and crooked elections (in guess who’s favor)
  • Hamas-sponsored riots and
  • anti-Semitic attacks on Jews in college campuses
  • eco-terrorism and obstructive demonstrations
  • violent demonstrations against public officials (e.g. Supreme Court justices) who dare to oppose their agenda
  • waste, abuse and outright fraud in the federal government budget
  • sending foreign aid money — by the billion — to sponsor overt anti-American activities abroad
  • siphoning “foreign aid” money — by the tens of millions — to line the pockets of executives running Washington D.C. non-profit organizations
  • a military weakened by woke DEI policies and regulations
  • a foreign policy that supports enemies of the U.S. (e.g. Iran) rather than chastises them
  • over-regulation of industry which chokes off economic progress
  • schools which have failed our children, and the government department that is responsible for that failure
  • a mandate that all cars sold in the U.S. be EVs, by 2030 — i.e. five years’ time — with no supporting infrastructure to sustain them
  • [insert your favorite issues here]

Seriously?  One in every five voters supports all the above?

Let me tell you right now:  it’s not 20%, but more like 5%.  In other words, the Democrats are supporting splinter issues that may find favor with only five in every hundred U.S. citizens — and even 5% may be too high.

So let’s quit this exaggeration of their support, please.  Most of their positions are deeply unpopular with almost all voters, and an “80/20” apportionment gives a misleading impression.  Numbers matter, so let’s start using the more-correct one.

Speaking of numbers, here’s a recent poll highlight:

When asked in an open-ended question to name the Democratic leader they feel “best reflects the core values” of the party, “10% of Democratic-aligned adults name New York Rep. Alexandria Ocasio-Cortez, 9% former vice president Kamala Harris, 8% Vermont Sen. Bernie Sanders and 6% House Minority Leader Hakeem Jeffries. Another 4% each name former president Barack Obama and Texas Rep. Jasmine Crockett, with Schumer joining a handful of others at 2%.”

When AOC is your standard-bearer (and the rest are equally dire)…

Let’s Hear It For The Pollsters

Elections, Journalist Scum, Morons & Idiots, Numbers & Statistics

I think this little debacle — initially seen in 2016 with Trump’s first electoral victory — can be summed up thus:

So much for them, then:  they were as clueless as all their US counterparts, all of whom called the election as “close” when (barring vote fraud) it was never going to be anything like that.

I know, I know:  everyone tries to hedge their bets in the prediction game, but never so egregiously.  It was obvious to any disinterested observer that they were cooking the  stats by slanted sampling and so on.

One would think that the pollsters would have learned their lesson from 2016, but noooo.

What I want to know is:  why should we believe anything these assholes tell us from now on?

Anyone?  Bueller?

Big Fat Duh

Lies and Untruths, Numbers & Statistics

There’s a great deal I know only a little about, still more about which I know nothing, and a terrifyingly-small number of things I know quite a lot about. [/Donald Rumsfeld]

But one of the things which fall into the latter category is that of statistical sampling, because my very first real job was in the Statistics Department of what was then the largest marketing research company in the world (the Great Big Research Company, or A.C. Nielsen).  And my specific area of expertise was in sample selection:  the methodology of creating a sample, the data drawn from which would accurately represent reality.  A single anecdote will suffice.

One of our major clients was the yogurt-producing subsidiary of a large dairy corporation (think: Yoplait).  Our data was always being questioned by this company, because in some cases we would show their market share as being too small (the sales numbers didn’t jibe with their actual deliveries to stores, for example —  a known quantity), or else, paradoxically, far too large, for exactly the same reason:  all dependent on which geographical area we were reporting on.

My job was to investigate this phenomenon, and some months later I discovered the reason.  The various smaller dairies’ yogurts were not being delivered to all the stores in the area, but in stores where they did have fridge space, they sold extremely well.  Using a simple picture shows the problem:

Our sample of stores may have been representative of say, total grocery sales in the area (and it was), but when Yogurt sales were carved out, the sample simply sucked because of how the dairies’ distribution worked.

It’s a very complex problem, and it applies to just about any sample selection.  In this case, there was no solution other than to broaden the sample, which would have cost too much.  So unless the client was prepared to pay a much higher fee to get better data, they’d either have to live with suspect data or cancel their account altogether.  (The end result was that they stopped looking at specific markets, and only bought data at the national level, which was acceptably accurate, but less useful to the local sales teams.)

I told you all that so I could talk about this.

Harris’ So-Called ‘Surge’ Is Thanks To Oversampling: Pollsters

In the meta data from the call centers college educated Dems are 3-4x more likely to answer than non-college. While weighting can help minimize the bias if done correctly it won’t totally eliminate the problem.
— Mark Davin Harris (@markdharris) August 16, 2024

Critics point out that many polls have been sampling a disproportionately smaller share of Republican voters compared to exit poll data from the 2020 presidential election. The result, they say, is a misleading “phantom advantage” for Ms. Harris. According to them, this skewed sampling could be a strategic move to boost enthusiasm and fundraising for Ms. Harris’ campaign.

Usually, when I talk about situations like this, I use a shorthand expression like:  “They must have drawn their sample from the Harvard Faculty Lounge.”

Unscrupulous polling companies can (and do) draw their samples to show exactly what the clients want to see — tailoring the samples to produce the desired results.  We used to call this the “K factor”:  that number which when applied to the data will provide the result most favorable to the client.  It’s more commonly known within the research community as “bullshit”, but it’s bullshit that will generate headlines — so ten guesses as to whether the mainstream media will accept such data uncritically, either because it favors their own bias/opinion or because they are completely incapable of analyzing the data properly.  (If you answered “or both” to the above, go to the head of the class.)

So is the “Kamala Surge” real, or not?  Given all the players in this particular piece of theater… oh please, it’s patent bullshit.

Unsurprising

Lies and Untruths, Numbers & Statistics

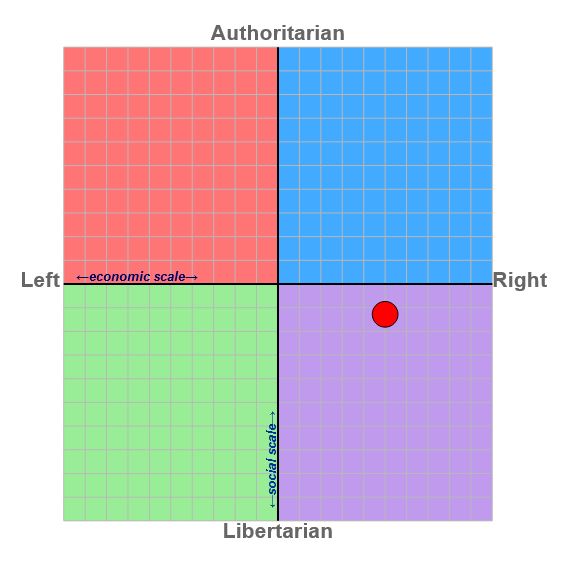
Given the observation that all Internet surveys on the topics of politics and economics will inevitably prove that you’re a libertarian, I nevertheless took this test:

My problem with these kinds of surveys is that questions are often posed demanding an either/or response, or else the question steers you towards a choice that isn’t really a choice

Here’s one example, in fact the very first question:

If economic globalisation is inevitable, it should primarily serve humanity rather than the interests of trans-national corporations.

If economic globalization occurs, it will largely be brought about by government and transnational corporations.  Expecting either to protect or enhance the interests of “humanity” is naïve beyond belief, because globalization is sought either for control (government) or profit (corporations).  You can’t actually answer that question inside an Agree / Disagree matrix.  But because the role of governments is ignored in the question, you’re forced into supporting transnational corporations or opposing them — a false dichotomy because in some cases, a uniform model is good (banking) or terrible (gun control).  (I know:  gun control isn’t an economic issue, unless one ignores H.L. Menken’s observation that when politicians talk, regardless of topic, it’s always about money.)

Here’s another:

Our race has many superior qualities, compared with other races.

Define “race”.  Are we using the classical definitions (e.g. Western-European, Sino-Japanese, Middle-Eastern) or the modern one (Black / White / Yellow / Other)?  The White “race” is superior to the Black race when it comes to things like fine art, architecture or the rule of law, but are those even “qualities”?  Once again, the survey-taker is left to decide what we’re talking about here, but in this case you can’t combine disparate definitions and opinions when using vague terminology.

One more example:

Controlling inflation is more important than controlling unemployment.

Those are incomparable conditions, because neither is a cause or a consequence, nor are they relatable.  And “more important” to whom, exactly?

Having worked in the research business for over a quarter-century, I’ve designed literally hundreds of surveys, and found the “agree/disagree” format to be profoundly inferior to discrete / conjoint analysis — the latter involving a set of choices on the same topic, e.g.

Which do you prefer:

Option A or Option B?
Option B or Option C?
Option A or Option C?

The problem with conjoint methodology is that it’s more difficult to set up and to analyze, so lazy researchers (i.e. most of them) tend to go with the simpler binary structure.

Life, unfortunately, is seldom binary (unless you are a computer, totalitarian, religious zealot, libertarian or idiot — some overlap).  The real world is more complex than that, which is why setting economics and social issues on a simple XY axis will almost always lead you to discover that Aha! you too are a libertarian, or would be if you could.

In fact, I have found that I tend more to the authoritarian side of the scale because I have to acknowledge that some form of outside control is sometimes  necessary — protection of private property and streetlights being the simplest ones to imagine — but it can equally be deplorable (e.g. Judenfrei  Nazi Art).

Nuance:  we all have it, in varying degrees, except to most survey-takers.

Please note that I’ve erred on the side of simplicity in the above, because nothing causes a MEGO reaction like a discussion of statistical methodology.  (MEGO:  my eyes glaze over.)

 

Reversed Immigration

Numbers & Statistics

Well now, lookee here:

Axios commissioned a Harris poll and discovered something unsurprising, even if the establishment was shocked. 

Americans support mass deportations of illegal aliens.

In case you couldn’t be bothered to follow the link, here’s the chart:

No surprises there, I suspect.

Also, when drilling further into the numbers it was discovered that all but one group showed a decrease in support, when it was explained that “deportation” might include this option:

I’ll leave it up to you to pick which group remained steadfast in their support.

…And For This One

Lies and Untruths, Military, Numbers & Statistics

Talking about the Huns fiddling with the numbers when the results aren’t to their liking:

The German army’s accuracy has again been mired in controversy as it was revealed in a classified report the testing for their latest rifle was lowered.

The G95A1 rifle failed to pass trials with military-standard ammunition so the Bundeswehr – the German army – lowered the standards of the test, the report stated.

The manufacturers of the rifle – Heckler and Koch – were allowed to test it with civilian ammunition and at room temperature rather than in extreme heat and cold.

The classified report read: ‘Current testing by the army in laboratory conditions shows that the weapon doesn’t meet army standards when loaded with combat ammunition.

‘The army requires an assault rifle that is sufficiently accurate under real conditions with its combat ammunition.’

The rifle was ordered to replace the G36 – also made by Heckler and Koch – which was dropped after it was found to become inaccurate after sustained firing. 

The G36’s inconsistency was down to a plastic channel that support the barrel would become soft when the gun heats in a quick succession of firing. 

The fault was first discovered when German soldiers serving in Afghanistan complained their guns were not shooting straight after a bout of heavy fire. 

As we all know, when the facts are uncomfortable and/or do not conform to the theory, they must be changed.  (I don’t know how that sounds in German, but I bet it’s lovely.)  Also:

Their 180,000-strong army is due to be receiving new weapons next year after it was reported that they only had enough ammunition to fight for two days.

However, the new gun’s accuracy is up to scratch according to Germany’s elite KSK troops who have been equipped with the G95A1. [as long as you only shoot it indoors — K.]

 A 2015 survey of German soldiers found that only 8 per cent of Bundeswehr soldiers trusted their weapons.

Somewhere out there, Paul Mauser is spinning in his grave.

I bet they’d even do better with one of these instead…

Looks like it’s not just German cars that are starting to suck.